REML 방법으로 분산 성분을 추정하는 세 가지 방법이 있다고 하였다. 1) derivative free, 미분하지 않고 그냥 분산 성분 찾아내기 2) 1차 미분하여 0과 같다고 놓고 분산 성분 찾아내기 3) 2차 미분하여 분산 성분 찾아내기.
2차까지 미분하는 이유는 1차 미분한 식에서 식을 0으로 하는 분산 성분 값을 찾기가 힘들고, 추정한 분산 성분을 이용하여 다시 육종가를 구하고 하는데 많은 round를 필요로 한다는 것이다. 원래 likelihood에서 최대 값을 찾기 위하여 1차 미분을 하였다면, 1차 미분 식을 0으로 만드는 값을 빨리 찾기 위하여 2차 미분을 하는 것이다. (자세한 사항은 나중에)
여기서는 1차 미분한 식을 이용하여 2차 미분한 식을 유도해 보고자 한다. 미분 기호식만 쓴다면 2차 미분은 매우 간단하다. 그래서 Johnson and Thomson의 Restricted maximum likelihood estimation of variance components for univariate animal models using sparse matrix techniques and average information 논문에는 다음과 같이 1차 미분식과 2차 미분식이 간단히 나온다.

그리고 Searle의 Variance Component라는 책에도 다음과 같이 나온다.
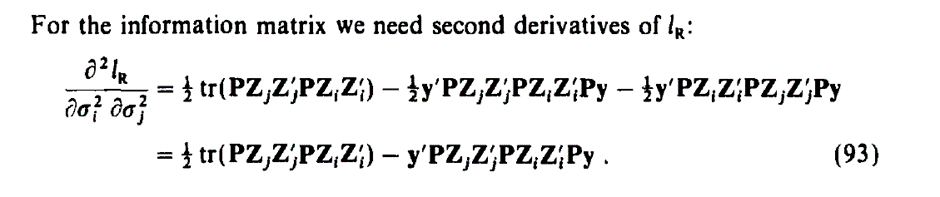
그러나 계산을 위해서 경우를 나누어 보면 약간 복잡해 진다. 분산을 효과의 분산과 잔차의 분산으로 나누어 본다면 1) 효과의 분산 - 효과의 분산으로 미분 2) 효과의 분산 - 잔차 분산으로 미분 3) 잔차 분산 - 잔차 분산으로 미분하는 경우로 나누어 볼 수 있다. 그래서 Gilmour의 Average Information REML An Efficient Algorithm for Variance Parameter Estimation in Linear Mixed Models 논문에서는 다음과 같이 2차 미분한 식을 다음과 같이 표현하고 있다.

그리고 Larry Schaeffer의 Animal Model and Estimation of Variance Components 라는 책에서는 다음과 같이 표현하고 있다.

여기서는 2차 미분식을 추정해 보는데 역시나 용어가 어렵다. 1차 미분한 식을 R. A. Fisher가 사용한 용어를 따라 Scoring function 등으로 부른다고 했는데 2차 미분한 식도 이름이 있다. Hessian Matrix. 그렇다면 우리가 구하는 식을 2차 미분한 식이라고 하였는데 Hessian Matrix를 구하는 것인가? 그렇지 않다. 우리가 구하는 식은 Hessian Matrix에 "-" negative를 붙인 식인데 이것을 observed information matrix (관측 정보 행렬???)이라고 한다. 비슷한 이름이 많고 헷갈린다. observed information matrix는 expected informaion matrix를 구하고 observed information matrix와 expected information matrix의 평균인 average information matrix를 구하는 기초가 된다. 여기서 matrix라는 표현을 쓰는데 효과의 분산이 한 개이고, 잔차 분산이 있는 경우 행렬의 (1,1) 원소는 잔차 분산 - 잔차 분산으로 미분한 경우의 값, (1, 2) 원소는 잔차 분산 - 효과의 분산으로 미분한 경우의 값 (2, 2) 원소는 효과의 분산 - 효과의 분산으로 미분한 경우의 값이다. information matrix의 역행렬을 구해서 빠르게 likelihood를 1차 미분한 식을 0으로 만드는 값을 찾는 방법은 나중에 설명하기로 한다. 암튼 여기서는 위 그림의 식을 유도한다.




notation의 약간의 차이가 있지만 암튼 유도를 마쳤다.
'Animal Breeding > REML Variance Component Estimation' 카테고리의 다른 글
| 평균 정보 행렬(average information matrix, AI matrix) (0) | 2025.10.29 |
|---|---|
| 기대 정보 행렬의 유도(derivation of expected information matrix) (0) | 2025.10.29 |
| REML log likelihood function을 미분하여 분산성분 추정하기(first derivatives of the natural log of the restricted likelihood function) (0) | 2025.09.18 |
| Derivative Free REML - Simplex Method (1) | 2025.08.30 |
| Derivative Free REML(REstricted Maximum Likelihood) (2) | 2025.08.28 |