REML의 likelihood function을 이용하여 분산 성분을 추정하는 방법에는 세 가지가 있다고 하였다. 1) 미분하지 않고 2) 1차 미분하고 3) 2차 미분하고.
앞의 포스트는 미분하지 않고 분산 성분을 추정하는 방법에 대한 포스트 였고, 여기서는 미분을 하고 0으로 놓아, likelihood fucntion을 최대로 하는 분산값을 찾는 방법을 설명한다. 미분 자체는 매우 간단하다. determinant의 로그값의 미분이나, 역행렬의 미분에 대해서는 이미 앞선 글에서 설명한 바 있다. 미분이 문제가 아니라 미분한 식을 계산 가능한 식으로 변환하는 것이 문제다. Projection Matrix P가 장악을 한 공식인데 이게 매우 복잡하여 실제로 계산을 하기에 적당하지 않아서, 이것을 계산이 가능한 적당한 식으로 변환하는 것이 문제다. 암튼 여러 참고 문헌과 AI의 도움으로 유도를 하였다. 여러 참고 문헌 중 S. R. Searle의 Variance Component란 책이 많은 도움이 되었다. 대학원생이라면 한 번 보겠지만 지금은 엄두가 나지 않는다.
100년 전에 R. A. Fisher는 log-likelohood function을 1차 미분한 것을 score function이라고 하였다. "추정량이 얼마나 잘 모수를 반영하는가"를 점수(score)처럼 매겨 평가한다는 개념적 비유가 사용된 것이라고 한다. 그래서 지금부터 어디선가 score function이란 말을 들어도 당황하지 말아야 겠다.
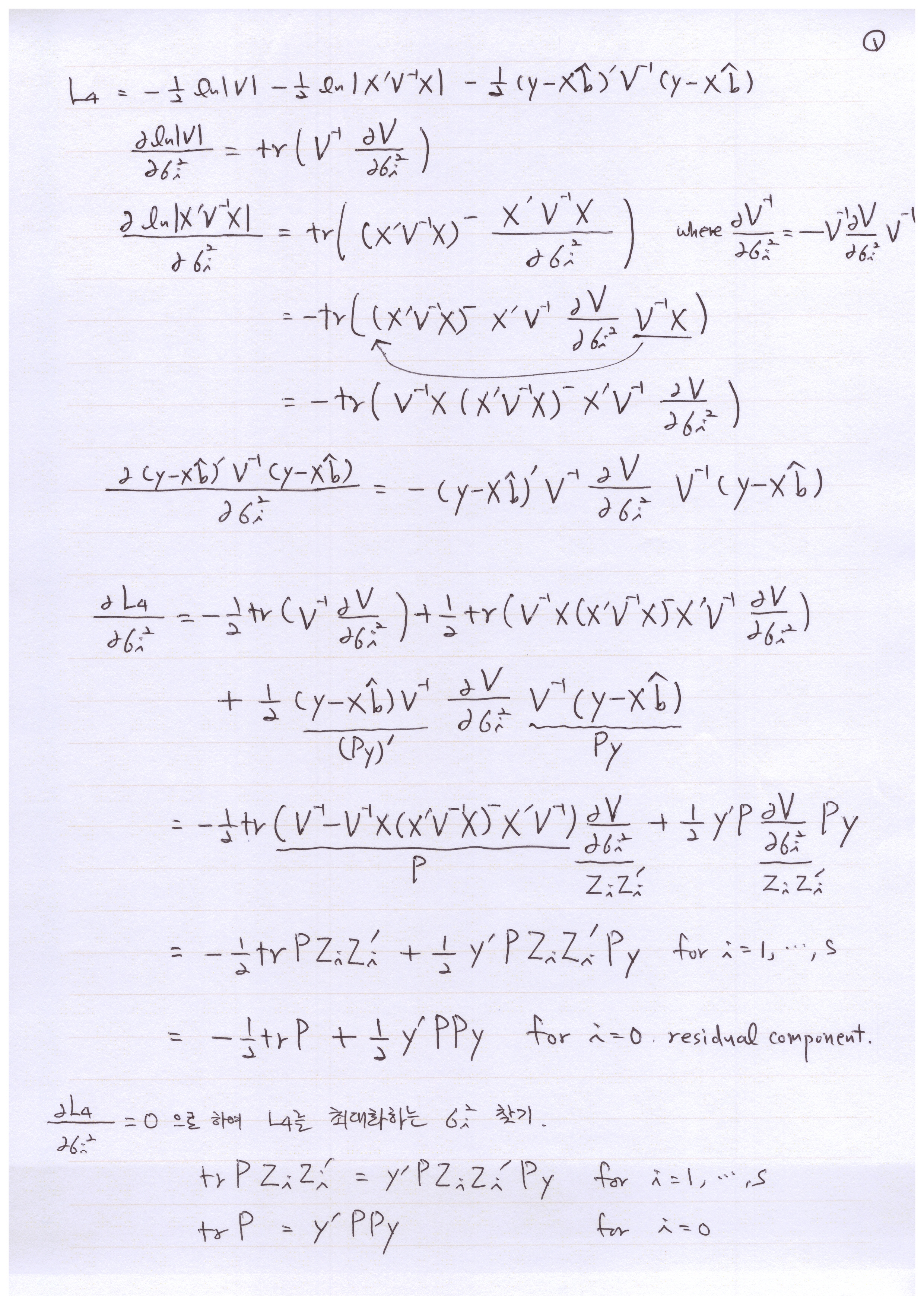
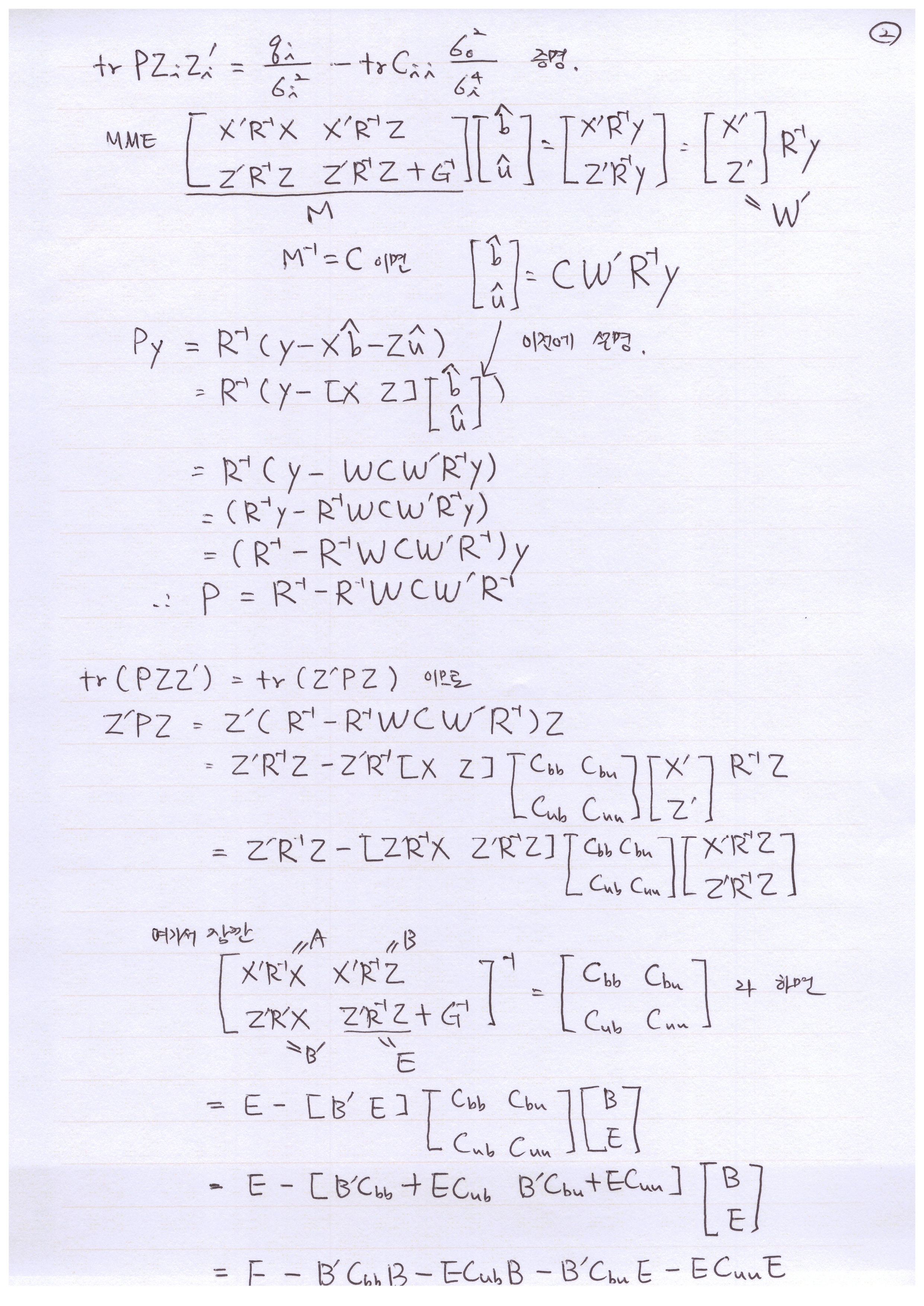



Expectation-Maximization Algorithm
이제 전에도 이용했던 예제를 이용하여 간단히 분산 성분을 추정해 보자.

90개의 자료를 이용하여 구성한 least squares equation이다. 고정효과 1개, 임의 효과 A와 B가 있으며, 고정 효과의 레벨 수(rank of X)는 2(r(X) = 2), 임의 효과의 A의 레벨 수는 3, 임의 효과 B의 레벨수는 4이다. 전체 관측치의 제곱합(total sum of squares)는 356,000이다.
임의 효과 A의 분산비 초기값은 10, 임의 효과 B의 분산비 초기값은 5로 하여, 해를 구하고(expectation), 그 해를 기초로 likelihood function을 최대화 하는 분산 성분을 추정(maximization)한다. 그리고 구한 분산 성분을 기초로 분산비를 구한 후, expectation - maximization을 반복한다. 수렴 기준(convergence criteria)을 정하고, 수렴할 때까지 반복한다.
# total sum of squares
yty = 356000
yty
# left hand side
lhs = matrix(c(
50, 0, 5, 15, 30, 5, 10, 20, 15,
0, 40, 5, 15, 20, 5, 10, 20, 5,
5, 5, 10, 0, 0, 2, 3, 4, 1,
15, 15, 0, 30, 0, 5, 7, 11, 7,
30, 20, 0, 0, 50, 3, 10, 25, 12,
5, 5, 2, 5, 3, 10, 0, 0, 0,
10, 10, 3, 7, 10, 0, 20, 0, 0,
20, 20, 4, 11, 25, 0, 0, 40, 0,
15, 5, 1, 7, 12, 0, 0, 0, 20
), nrow = 9, byrow = TRUE)
lhs
# right hand side
rhs = matrix(c(3200, 2380, 580, 1860, 3140, 700, 1320, 2400, 1160), nrow = 9)
rhs
# variance ratio
# alpha_a = 40, alpha_b = 10 일 때
alpha_a = 10
alpha_b = 5
lhs2 = lhs
# 임의효과에 분산비 더하기
diag(lhs2)[3:5] = diag(lhs2)[3:5] + alpha_a
diag(lhs2)[6:9] = diag(lhs2)[6:9] + alpha_b
lhs2
# solution 구하기
C = solve(lhs2)
#sol = solve(lhs2, rhs)
sol = C %*% rhs
sol
# rank
N_rx = 88
N_rx
# y'XbZu
ytXbZu = t(sol) %*% rhs
ytXbZu
# trCaa
trCaa = sum(diag(C)[3:5])
trCaa
# trCbb
trCbb = sum(diag(C)[6:9])
trCbb
# sigma_e2 추정
sigma_e2 = (yty - ytXbZu ) / N_rx
sigma_e2
# sigma_A2 추정
sigma_A2 = (t(sol[3:5]) %*% sol[3:5] + trCaa * sigma_e2) / 3
sigma_A2
# sigma_B2 추정
sigma_B2 = (t(sol[6:9]) %*% sol[6:9] + trCbb * sigma_e2) / 4
sigma_B2
# new ratio
alpha_a2 = sigma_e2 / sigma_A2
alpha_a2
alpha_b2 = sigma_e2 / sigma_B2
alpha_b2
실행 결과
> # total sum of squares
> yty = 356000
> yty
[1] 356000
>
> # left hand side
> lhs = matrix(c(
+ 50, 0, 5, 15, 30, 5, 10, 20, 15,
+ 0, 40, 5, 15, 20, 5, 10, 20, 5,
+ 5, 5, 10, 0, 0, 2, 3, 4, 1,
+ 15, 15, 0, 30, 0, 5, 7, 11, 7,
+ 30, 20, 0, 0, 50, 3, 10, 25, 12,
+ 5, 5, 2, 5, 3, 10, 0, 0, 0,
+ 10, 10, 3, 7, 10, 0, 20, 0, 0,
+ 20, 20, 4, 11, 25, 0, 0, 40, 0,
+ 15, 5, 1, 7, 12, 0, 0, 0, 20
+ ), nrow = 9, byrow = TRUE)
> lhs
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
[1,] 50 0 5 15 30 5 10 20 15
[2,] 0 40 5 15 20 5 10 20 5
[3,] 5 5 10 0 0 2 3 4 1
[4,] 15 15 0 30 0 5 7 11 7
[5,] 30 20 0 0 50 3 10 25 12
[6,] 5 5 2 5 3 10 0 0 0
[7,] 10 10 3 7 10 0 20 0 0
[8,] 20 20 4 11 25 0 0 40 0
[9,] 15 5 1 7 12 0 0 0 20
>
> # right hand side
> rhs = matrix(c(3200, 2380, 580, 1860, 3140, 700, 1320, 2400, 1160), nrow = 9)
> rhs
[,1]
[1,] 3200
[2,] 2380
[3,] 580
[4,] 1860
[5,] 3140
[6,] 700
[7,] 1320
[8,] 2400
[9,] 1160
>
> # variance ratio
> # alpha_a = 40, alpha_b = 10 일 때
> alpha_a = 10
> alpha_b = 5
>
> lhs2 = lhs
>
> # 임의효과에 분산비 더하기
> diag(lhs2)[3:5] = diag(lhs2)[3:5] + alpha_a
> diag(lhs2)[6:9] = diag(lhs2)[6:9] + alpha_b
>
> lhs2
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
[1,] 50 0 5 15 30 5 10 20 15
[2,] 0 40 5 15 20 5 10 20 5
[3,] 5 5 20 0 0 2 3 4 1
[4,] 15 15 0 40 0 5 7 11 7
[5,] 30 20 0 0 60 3 10 25 12
[6,] 5 5 2 5 3 15 0 0 0
[7,] 10 10 3 7 10 0 25 0 0
[8,] 20 20 4 11 25 0 0 45 0
[9,] 15 5 1 7 12 0 0 0 25
>
> # solution 구하기
> C = solve(lhs2)
> #sol = solve(lhs2, rhs)
> sol = C %*% rhs
> sol
[,1]
[1,] 64.6313096
[2,] 59.4225059
[3,] -2.1363094
[4,] 0.4994633
[5,] 1.6368461
[6,] 5.1063791
[7,] 2.6402428
[8,] -2.6432515
[9,] -5.1033704
>
> # rank
> N_rx = 88
> N_rx
[1] 88
>
> # y'XbZu
> ytXbZu = t(sol) %*% rhs
> ytXbZu
[,1]
[1,] 347871.3
>
>
> # trCaa
> trCaa = sum(diag(C)[3:5])
> trCaa
[1] 0.1649312
>
> # trCbb
> trCbb = sum(diag(C)[6:9])
> trCbb
[1] 0.3309886
>
> # sigma_e2 추정
> sigma_e2 = (yty - ytXbZu ) / N_rx
> sigma_e2
[,1]
[1,] 92.37198
>
> # sigma_A2 추정
> sigma_A2 = (t(sol[3:5]) %*% sol[3:5] + trCaa * sigma_e2) / 3
> sigma_A2
[,1]
[1,] 7.575855
>
> # sigma_B2 추정
> sigma_B2 = (t(sol[6:9]) %*% sol[6:9] + trCbb * sigma_e2) / 4
> sigma_B2
[,1]
[1,] 24.16281
>
> # new ratio
> alpha_a2 = sigma_e2 / sigma_A2
> alpha_a2
[,1]
[1,] 12.19294
>
> alpha_b2 = sigma_e2 / sigma_B2
> alpha_b2
[,1]
[1,] 3.822899
계속 반복하면 임의 효과 A의 분산비는 35.7558로, 임의 효과 B의 분산비는 3.0101로 수렴한다.
위에서는 분산 성분을 추정할 때 추정하려는 효과의 분산 공분산 행렬을 ZZ'로 가정을 했으나 가축 육종의 Animal Model에서는 A로 가정한다. A는 Numerator Relationship Matrix이다. 이것을 한국어로 혈연 계수 행렬로 번역을 하고 있으나 이는 사실과 다르다. 정확히는 혈연 계수의 분자의 행렬이다. A로부터 혈연 계수를 구하려면 off diagonal의 숫자에 두 개체의 근교 계수의 root 값으로 나누어 주어야 한다. 그러나 너무 말이 복잡하므로 그냥 혈연 계수 행렬로 번역을 하는데 정확히 알아두는게 좋을 것 같다. Animal Model에서 개체 효과의 분산 공분산 행렬을 A라고 하였으므로 그것을 반영한 분산 성분 추정이어야 한다. 위에서 잔차의 분산은 변함이 없고 오로지 개체의 효과만 약간의 수정이 있다. 만일 repeatabiliy model 일 경우 영구 환경 효과 P를 고려하는데 MME와 개체의 분산 성분 추정을 위한 식은 다음과 같아 진다.

개체의 분산 성분을 추정할 때 A의 역행렬이 동원되는 것을 알 수 있다. 컴퓨팅 자원이 부족한 시절, A의 역행렬을 구하는 것은 매우 어려운 일이었다. 그런데 C. R. Henderson이 혈통을 보고 바로 A의 역행렬을 구하는 방법을 제시했다. MME를 제시하고, A의 역행렬을 바로 구할 수 있게 됨으로써 육종학의 새로운 지평이 열린 것이다.
'Animal Breeding > REML Variance Component Estimation' 카테고리의 다른 글
| 기대 정보 행렬의 유도(derivation of expected information matrix) (0) | 2025.10.29 |
|---|---|
| 관측 정보 행렬의 유도(derivation of observed information matrix) (0) | 2025.10.24 |
| Derivative Free REML - Simplex Method (1) | 2025.08.30 |
| Derivative Free REML(REstricted Maximum Likelihood) (2) | 2025.08.28 |
| Log Likelihood Function of REML(restricted maximum likelihood) (3) | 2025.08.25 |